مثالهای کاربردی
به منظور نمایش نحوه تحلیل سازههای نامعین استاتیکی با عضوهای تحت نیروهای محوری، به تشریح دو مثال کاربردی میپردازیم.
مثال 1
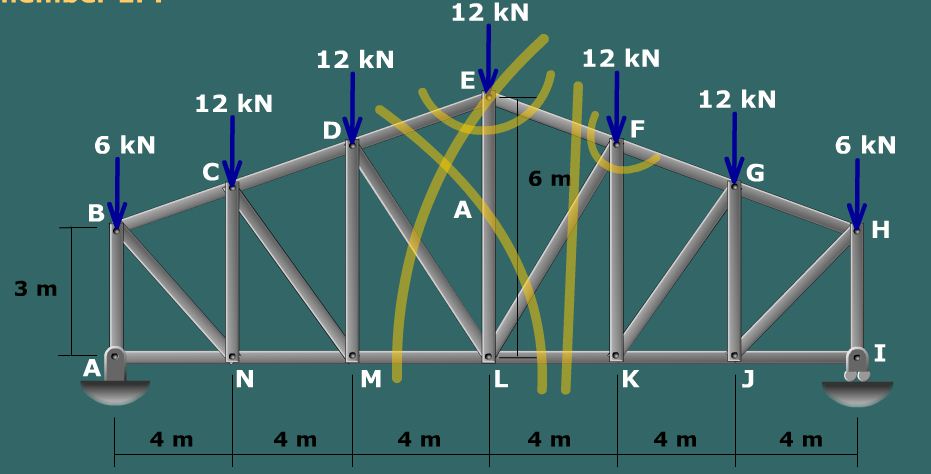
شکل زیر، یک سیلندر فولادی (S) را نمایش میدهد که درون یک لوله مسی توخالی (C) قرار گرفته است. سیلندر و لوله بین دو صفحه صلبِ یک دستگاه آزمایش قرار داده شدهاند. نیروهای فشاری P از صفحه بالایی به مجموعه سیلندر و لوله اعمال میشوند. As، مساحت سطح مقطع سیلندر، Es، مدول الاستیسیته فولاد، Ac، مساحت سطح مقطع لوله، Ec، مدول الاستیسیته مس و L، طول هر دو بخش مجموعه را نمایش میدهد. با توجه به اطلاعات مسئله، کمیتهای زیر را تعیین کنید:
- الف) نیروهای فشاری Psدر سیلندر فولادی و Pcدر لوله مسی
- ب) تنشهای فشاری ناشی از اعمال نیرو (σsو σc)
- ج) میزان کاهش طول مجموعه δ
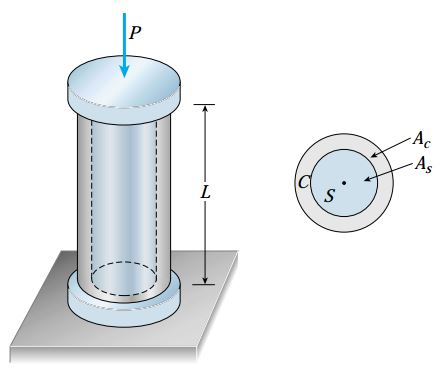
الف) تعیین نیروهای فشاری موجود در سیلندر فولادی و لوله مسی
در ابتدای کار به منظور نمایش نیروهای فشاری اعمال شده بر روی سیلندر فولادی و لوله مسی (Psو Pc)، صفحه بالایی مجموعه بالا را حذف میکنیم (شکل زیر). نیروی Ps، برآیند تنشهای یکنواخت اعمال شده بر روی سطح مقطع سیلندر فولادی و نیروی Pc، برآیند تنشهای اعمال شده بر روی لوله مسی است.
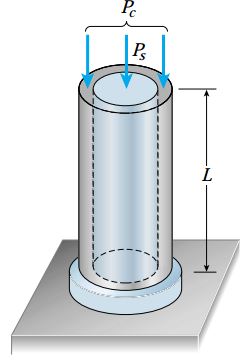
معادله تعادل
شکل زیر، نمودار جسم آزاد صفحه بالایی مجموعه را نمایش میدهد. این صفحه در معرض نیروی معلوم P و نیروهای مجهول Psو Pcقرار دارد.

با توجه به نمودار جسم آزاد صفحه، معادله تعادل زیر به دست میآید:

به دلیل وجود دو مجهول و یک معادله، سازه مورد تحلیل از نظر استاتیکی نامعین است.
معادله سازگاری
به دلیل صلب بودن صفحات انتهایی مجموعه، میزان کاهش طول سیلندر (δs) با میزان کاهش طول لوله (δc) برابر خواهد بود. به این ترتیب، معادله سازگاری به صورت زیر نوشته میشود:
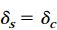
روابط نیرو-جابجایی
میزان تغییر طول سیلندر و لوله از طریق معادله کلی δ=PL/EA قابل محاسبه است. در این مثال، روابط نیرو-جابجایی به صورت زیر خواهند بود:
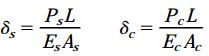
حل معادلات
اکنون معادلات بالا را به طور همزمان حل میکنیم. با جایگذاری روابط نیرو-جابجایی در معادله سازگاری، به رابطه زیر میرسیم:
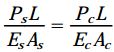
رابطه بالا، شرایط سازگاری را بر حسب نیروهای مجهول بیان میکند. در مرحله بعد، معادله تعادل و رابطه بالا را به طور همزمان حل میکنیم. به این ترتیب، روابط نیروهای محوری درون سیلندر و لوله به دست میآیند:
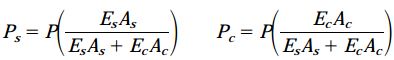
بر اساس این معادلات، هر یک از نیروهای فشاری در بخشهای فولادی و مسی با صلبیت محوری (EA) خود رابطه مستقیم و با مجموعِ صلبیتهای محوری رابطه عکس دارند.
ب) تنشهای فشاری موجود در سیلندر فولادی و لوله مسی
با مشخص شدن نیروهای محوری، تنشهای فشاری موجود در دو بخش مجموعه به صورت زیر تعیین میشوند:
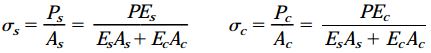
توجه داشته باشید که نسبت تنشهای σs/σcبا نسبت مدولهای الاستیسیته Es/Ec برابر است. این مسئله نشان میدهد که معمولاً ماده سختتر، تنشهای بیشتری را تحمل میکند.
ج) میزان کاهش طول مجموعه
به منظور تعیین میزان کاهش طول کل مجموعه میتوانیم از روابط نیرو-جابجایی استفاده کنیم. به این ترتیب، با جایگذاری نیروهای به دست آمده در این روابط خواهیم داشت:
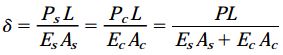
رابطه بالا نشان میدهد که میزان کاهش طول کل مجموعه از تقسیم بار کل بر جمع سختی دو بخش به دست میآید (سختی یک میله تحت بار محوری از رابطه k=EA/L محاسبه میشود).
استفاده از روشهای دیگر برای حل معادلات
در مراحل قبلی میتوانستیم به جای جایگذاری روابط نیرو-جابجایی در معادله سازگاری، آن روابط را به صورت زیر بازنویسی کنیم:
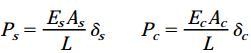
اکنون، با قرار دادن روابط بالا در معادله تعادل به معادله زیر میرسیم:

این معادله، شرایط تعادل را بر حسب جابجاییهای مجهول بیان میکند. با حل همزمان معادله سازگاری و معادله بالا، رابطهای برای تعیین جابجاییها به دست میآید:
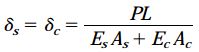
این رابطه با رابطه معرفی شده در روش قبل یکسان است. به این ترتیب، با تعیین مقادیر جابجاییهای مجهول و قرار دادن آنها در روابط Psو Pc، مقادیر نیروهای فشاری نیز مشخص میشوند.
توجه: روش جایگزینی که برای این مثال معرفی کردیم، نسخه سادهشدهای از روش تحلیل سختی یا جابجایی است. روش اول نیز نسخه سادهشدهای از روش انعطافپذیری یا نیرو را نمایش میدهد. در واقع، نامگذاری این روشها به دلیل در نظر گرفتن نیروها به عنوان مجهولات و انعطافپذیریها به عنوان ضرایب مسئله (در روش اول) و همچنین در نظر گرفتن جابجاییها به عنوان مجهولات و سختیها به عنوان ضرایب مسئله (در روش دوم) صورت گرفته است.
مثال 2
شکل زیر، یک میله افقی صلب را نمایش میدهد. این میله (AB) در نقطه A به یک تکیهگاه مفصلی متصل شده است. دو سیم CD و EF نیز در نقاط D و F از میله AB نگهداری میکنند. به علاوه، بار عمودی P در نقطه B به میله وارد میشود.
طول میله برابر با 3b و طول سیمهای CD و EF به ترتیب برابر با L1و L2است. با در نظر گرفتن قطر d1و مدول الاستیسیته E1برای سیم L1و قطر d2و مدول الاستیسیته E2برای سیم EF، موارد الف و ب را تعیین کنید.
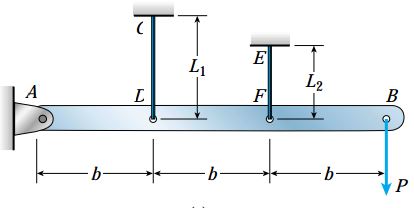
- الف) اگر تنشهای مجاز درون سیمهای CD و EF به ترتیب σ1 و σ1 باشند، فرمولهای مورد نیاز برای محاسبه بار مجاز P را به دست بیاورید. (از وزن میله صرف نظر کنید.)
- ب) اگر سیم CD از جنس آلومینیوم با مدول الاستیسیته E1=72GPa، قطر d1=4mm و طول L1=0.4m و سیم EF از جنس منیزیوم با مدول الاستیسیته E2=45GPa، قطر d2=3mm و طول L2=0.3m باشد، مقدار بارِ مجاز P چقدر خواهد بود؟ (تنشهای مجاز در سیمها آلومینیومی و منیزیومی را به ترتیب برابر با σ1=200MPa و σ2=175MPa در نظر بگیرید.)
معادله تعادل
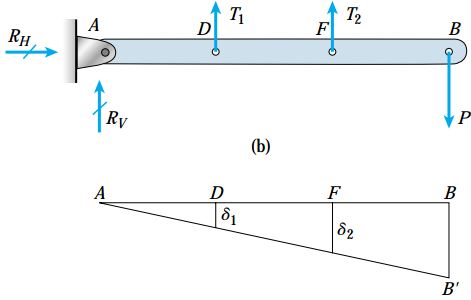
تحلیل این مسئله را با رسم نمودار جسم آزاد میله AB شروع میکنیم. T1 و T2 در این نمودار، نیروهای کششی مجهول در سیمهای CD و EF را نمایش میدهند. RH و RV نیز به ترتیب مؤلفههای افقی و عمودی عکسالعمل تکیهگاهی سازه هستند. به دلیل وجود چهار مجهول (T2 ،T1 ،RH و RV) و تنها سه معادله تعادل (گشتاور حول نقطه A، جمع مولفههای افقی نیرو و جمع مولفههای عمودی نیرو)، سازه مورد تحلیل از نظر استاتیکی نامعین در نظر گرفته میشود.

سازههای نامعین استاتیکی
با تعیین گشتاورهای موجود حول نقطه A، رابطه زیر به دست میآید (علامت گشتاور پادساعتگرد، مثبت در نظر گرفته میشود):
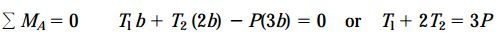
دو معادله مربوط به جمع نیروهای موجود در راستای افقی و همچنین جمع نیروهای موجود در راستای عمودی، هیچ کاربردی در تعیین T1 و T2 نخواهند داشت.
معادله سازگاری
بارِ P باعث دوران میله AB حول نقطه A و کشیدگی سیمهای CD و EF میشود. شکل جابجاییهای به وجود آمده را میتوان در نمودار جابجایی زیر مشاهده کرد. خط AB، موقعیت اولیه میله و خط A’B، موقعیت میله پس از جابجایی را نمایش میدهد. جابجاییهای δ1 و δ2 نیز معرف افزایش طولهای سیمهای CD و EF هستند. به دلیل کوچک بودن این جابجاییها، میله تحت یک زاویه بسیار کوچک دوران میکند. به همین دلیل میتوانیم در محاسبات خود فرض کنیم که حرکت رو به پایین نقاط F ،D و B به صورت عمودی است (نه به صورت دایرهای).
سازههای نامعین استاتیکی
به دلیل برابر بودن فواصل افقی AD و DF میتوانیم رابطه هندسی زیر را بین مقادیر افزایش طول در نظر بگیریم:
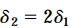
این معادله، معادله سازگاری مسئله مورد تحلیل است.
روابط نیرو-جابجایی
سیمهای CD و EF به صورت الاستیک خطی رفتار میکنند. از اینرو میتوان تغییر طولهای به وجود آمده در آنها را بر حسب T1 و T2 بیان کرد:
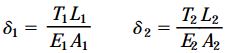
مساحت سطح مقطع سیمهای CD و EF از طریق روابط زیر به دست میآیند:

به منظور سادهسازی نحوه نوشتن معادلات، از مفهوم انعطافپذیری سیمها استفاده میکنیم:

به این ترتیب، روابط نیرو-جابجایی به فرم زیر تبدیل میشوند:

حل معادلات
اکنون میتوانیم معادلات و روابط بخشهای قبلی را به طور همزمان حل کنیم. برای شروع، روابط نیرو-جابجایی را در معادله سازگاری قرار میدهیم:
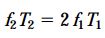
در معادله بالا و معادله تعادل، نیروهای T1 و T2 به عنوان کمیتهای مجهول به حساب میآیند. با حل همزمان این دو معادله بر حسب نیروهای مجهول به روابط زیر میرسیم:

با مشخص شدن T1 و T2 میتوانیم تغییر طول سیمها را با استفاده از روابط نیرو-جابجایی به راحتی تعیین کنیم.
الف) بار مجاز P
در بخش قبلی، تحلیل نامعین استاتیکی را انجام دادیم و روابط مربوط به نیروهای موجود در سیمها را به دست آوردیم. در این بخش، مقادیر مجاز بارِ P را مشخص میکنیم. تنش σ1 در سیم CD و تنش σ2 در سیم EF از طریق روابط ارائه شده برای T1 و T2 تعیین میشوند:
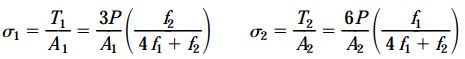
با استفاده از معادله اول میتوان مقدار مجاز نیروی P1 را بر حسب تنش مجاز σ1 در CD محاسبه کرد:
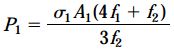
به همین ترتیب، مقدار مجاز P2 بر حسب تنش مجاز σ2 در سیم EF نیز به دست میآید:

از بین P1 و P2، هر کدام که مقدار کوچکتر داشته باشد به عنوان حداکثر بار مجاز (Pallow) انتخاب میشود.
ب) محاسبات عددی بار مجاز
اکنون با استفاده از اطلاعات مسئله و معادلات به دست آمده، مقادیر عددی کمیتهای مورد نیاز را محاسبه میکنیم:

علاوه بر موارد فوق، تنشهای مجاز نیز برابر با مقادیر زیر هستند:
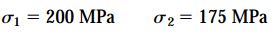
با جایگذاری این تنشها در روابط P1 و P2، مقدار بار مجاز در هر یک از سیمها مشخص میشود:
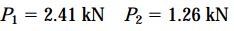
بار P1 بر اساس تنشهای مجاز در سیم آلومینیومی و بار P2 بر اساس تنشهای مجاز در سیم منیزیومی به دست آمده است. از بین این دو، مقدار کوچکتر به عنوان بار مجاز سازه در نظر گرفته میشود:
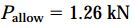
در بار مجاز (Pallow=1.26kN)، تنش درون سیم منیزیمی 175 مگاپاسکال (مقدار مجاز) و تنش درون سیم آلومینیومی (1.26/2.41)*200=105 مگاپاسکال است. همانطور که انتظار میرفت، مقدار این تنش کمتر از تنش مجاز 200 مگاپاسکالی شد.