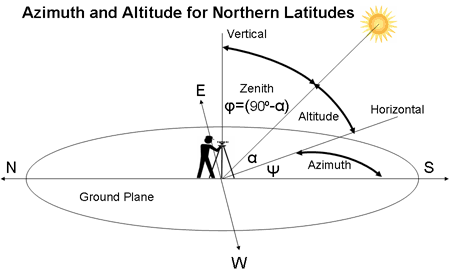
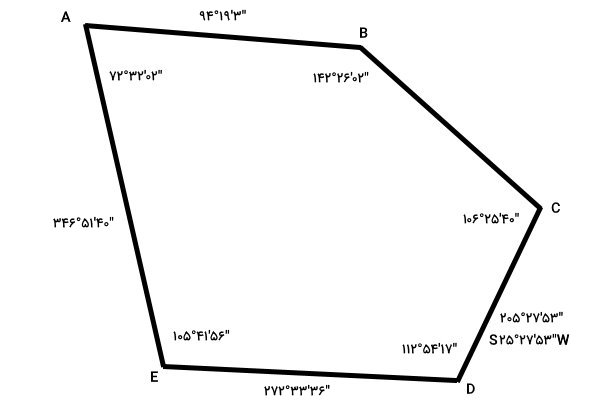
آزیموت، یکی از ابزارهای کاربردی برای مشخص کردن و نمایش جهتها است. در نقشهبرداری و پیمایش مرزهای یک محدوده، آزیموت، امتداد هر ضلع را مشخص میکند. محاسبه آزیموت در نقشه برداری، قواعد و اصول مخصوص به خود را دارد. در این بخش، این قواعد را به همراه یک مثال توضیح میدهیم. تصویر زیر، محدوده یک پیمایش بسته را نمایش میدهد. بیرینگ یکی از ضلعهای محدوده در کنار آن نوشته شده است. اعداد کنار رئوس، اندازه زوایای داخلی هستند. قصد داریم با این اطلاعات، آزیموت ضلعهای دیگر پیمایش را به دست بیاوریم.
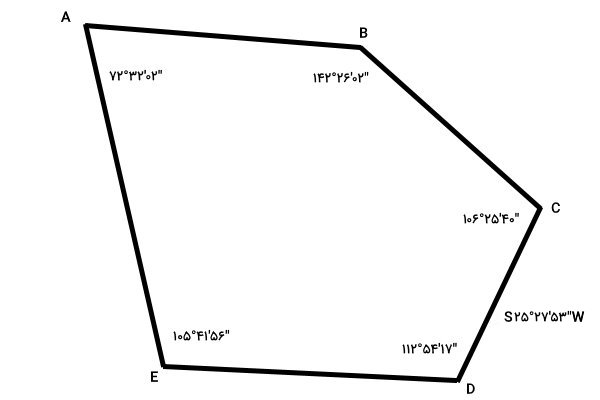
اندازهگیری آزیموت، در هر دو جهت ساعتگرد و پادساعتگرد قابل انجام است. برای حل این مثال، هر دوی این روشها را توضیح میدهیم. در ابتدا، به آموزش نحوه محاسبه آزیموت در نقشه برداری در جهت ساعتگرد میپردازیم.
تبدیل بیرینگ به آزیموت
اندازه بیرینگ یکی از خطوط پیمایش را داریم:
S۲۵°۲۷’۵۳”W = بیرینگ خط امتداد مبنا
برای تبدیل بیرینگ به آزیموت، ربع قرارگیری آن را تعیین میکنیم. این برینگ در ربع سوم (NW) قرار دارد. رابطه تبدیل آزیموت به بیرینگ عبارت است از:
۱۸۰° – آزیموت = بیرینگ
مقدار عددی بیرینگ (یعنی ۲۵) را درون رابطه بالا قرار میدهیم:
۱۸۰° – آزیموت = “۵۳’۲۷°۲۵
“۵۳’۲۵°۲۷ + ۱۸۰° = آزیموت
“۵۳’۲۰۵°۲۷ = آزیموت
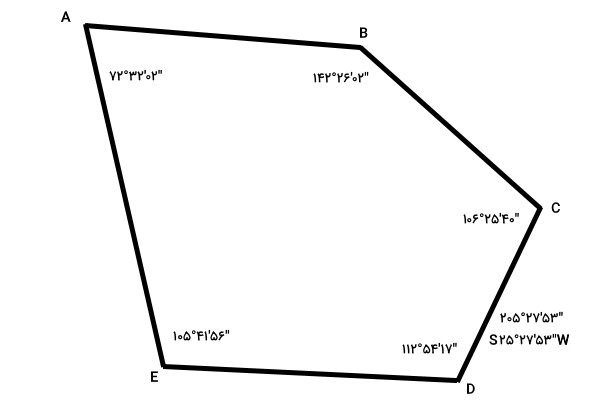
آزیموت امتداد اولین خط را به دست آوردیم. اکنون میتوانیم به سراغ آزیموت و بیرینگ خطوط دیگر پیمایش بریم.
تعیین جهت و نحوه انجام محاسبات
پیش از محاسبه آزیموت دیگر خطوط، ابتدا جهت جهت انجام محاسبات را مشخص میکنیم. در مرحله قبل، آزیموت یکی از خطوط را به دست آوردیم. این آزیموت، مبنای شروع محاسبات و برابر با “۵۳’۲۷°۲۰۵ است. بر اساس ربع قرارگیری بیرینگ، میتوانیم بگوئیم که جهت شمال، به سمت بالای نقشه اشاره میکند. جهت شمال را بر روی ضلع CD در نظر بگیرید.
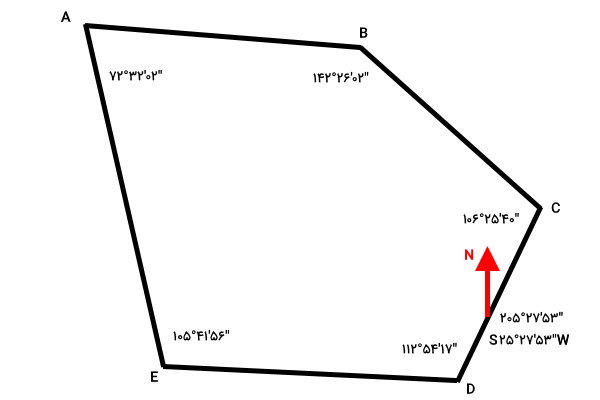
با توجه به تعریف آزیموت، زاویه بین جهت شمال و خط CD در جهت حرکت عقربههای ساعت برابر با “۵۳’۲۷°۲۰۵ است. بنابراین، جهت حرکت ما از C به D خواهد بود. به این ترتیب، در قدم بعدی باید به سمت نقطه E، نقطه A، نقطه B برویم و در انتها به نقطه C بازگردیم. این جهت، ساعتگرد است.
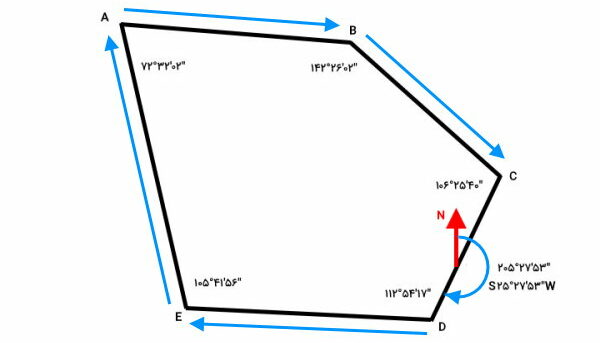
فرمول های محاسبه آزیموت در نقشه برداری
محاسبه آزیموت در یک پیمایش بسته، با توجه به آزیموت امتداد معلوم، آزیموت عقب امتداد معلوم، زوایای داخلی و جهت حرکت انجام میگیرد. در صورت ساعتگرد بودن جهت حرکت، آزیموت هر امتداد با تفریق زاویه داخلی از آزیموت عقب امتداد مجاور محاسبه میشود:
آزیموت امتداد دوم =
زاویه داخلی بین دو امتداد – آزیموت عقب امتداد اول
اگر جهت حرکت پادساعتگرد باشد، آزیموت هر امتداد از جمع زاویه داخلی با آزیموت عقب امتداد مجاور به دست میآید:
آزیموت امتداد دوم =
زاویه داخلی بین دو امتداد + آزیموت عقب امتداد اول
با توجه به روابط بالا، به سراغ محاسبه آزیموت دیگر خطوط پیمایش در این مثال میرویم.
محاسبه آزیموت خطوط پیمایش در جهت ساعتگرد
پس از تعیین جهت انجام محاسبات، به سراغ تعیین آزیموت امتداد خط DE میرویم. در بخش قبلی گفتیم که به دلیل ساعتگرد بودن جهت حرکت، فرمول محاسبه آزیموت برابر خواهد بود:
آزیموت امتداد دوم =
زاویه داخلی بین دو امتداد – آزیموت عقب امتداد اول
به عبارت دیگر، داریم:
زاویه بین CD و DE – آزیموت عقب CD = آزیموت DE
زاویه داخلی بین CD و DE برابر با “۱۷’۵۴°۱۱۲ است. آزیموت عقب CD نیز با توجه ربع قرارگیری آن (ربع سوم) به صورت زیر محاسبه میشود:
۱۸۰° – آزیموت جلو = آزیموت عقب
۱۸۰° – “۵۳’۲۰۵°۲۷ = آزیموت عقب CD
“۵۳’۲۵°۲۷ = آزیموت عقب CD
اکنون این مقادیر را در رابطه آزیموت DE قرار میدهیم:
(“۱۷’۱۲۷°۵۴) – “۵۳’۲۵°۲۷ = آزیموت DE
جواب رابطه بالا، منفی میشود. میدانیم که آزیموت، بین ۰ تا ۳۶۰ درجه است. از اینرو، برای جلوگیری از منفی شدن محاسبات بالا، ۳۶۰ به آن اضافه میکنیم:
“۰’۳۶۰°۰ + (“۱۷’۱۲۷°۵۴) – “۵۳’۲۵°۲۷ = آزیموت DE
“۳۶’۲۷۲°۳۳ = آزیموت DE
به این ترتیب، آزیموت DE برابر با “۳۶’۳۳°۲۷۲ میشود. از این آزیموت برای به دست آوردن آزیموت امتداد بعدی، یعنی امتداد EA استفاده میکنیم.
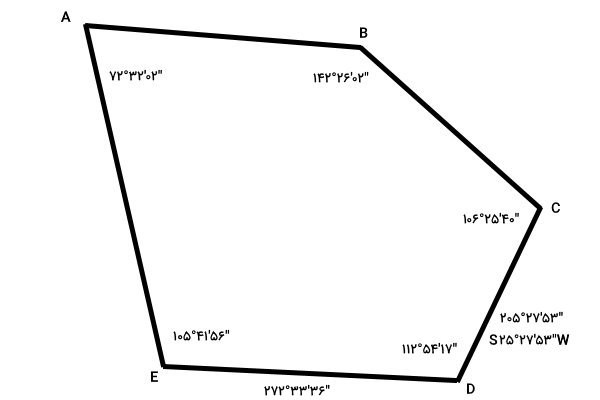
زاویه داخلی بین DE و EA برابر با “۵۶’۴۱°۱۰۵ است. آزیموت عقب امتداد DE نیز از رابطه زیر به دست میآید:
۱۸۰° – “۳۶’۲۷۲°۳۳ = آزیموت عقب DE
“۳۶’۹۲°۳۳ = آزیموت عقب DE
اکنون، مقادیر معلوم را درون رابطه آزیموت EA قرار میدهیم. این رابطه به صورت زیر نوشته میشود:
زاویه بین DE و EA – آزیموت عقب DE = آزیموت EA
(“۵۶’۱۰۵°۴۱) – “۳۶’۹۲°۳۳ = آزیموت EA
دقیقا مانند آزیموت DE، جواب محاسبات بالا، منفی است. بنابراین، ۳۶۰ درجه به آن اضافه میکنیم:
“۰’۳۶۰°۰ + (“۵۶’۱۰۵°۴۱) – “۳۶’۹۲°۳۳ = آزیموت EA
“۴۰’۳۴۶°۵۱ = آزیموت EA
بنابراین، آزیموت امتداد EA برابر با “۴۰’۵۱°۳۴۶ شد. اکنون به سراغ آزیموت امتداد خط بعدی پیمایش، یعنی خط AB میرویم.
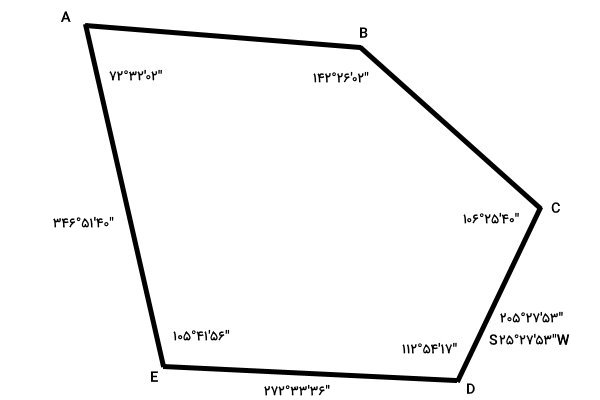
زاویه داخلی بین EA و AB برابر با “۰۲’۳۲°۷۲ است. آزیموت عقب امتداد EA از رابطه زیر حساب میشود:
۱۸۰° – “۴۰’۳۴۶°۵۱ = آزیموت عقب DE
“۴۰’۱۶۶°۵۱ = آزیموت عقب DE
از آزیموت عقب و زاویه داخلی برای محاسبه آزیموت AB استفاده میکنیم:
زاویه بین EA و AB – آزیموت عقب EA = آزیموت AB
“۰۲’۷۲°۳۲ – “۴۰’۱۶۶°۵۱ = آزیموت AB
به دلیل مثبت بودن نتیجه محاسبات بالا، در اینجا دیگر نیازی به اضافه کردن ۳۶۰ درجه نداریم. بنابراین:
“۳۸’۹۴°۱۹ = آزیموت AB
از اینرو، آزیموت امتداد AB برابر با “۳۸’۱۹°۹۴ است. این آزیموت را مبنای محاسبه آزیموت امتداد BC قرار میدهیم.
زاویه داخلی بین AB و BC برابر با “۰۲’۲۶°۱۴۲ است. آزیموت عقب امتداد AB توسط فرمول زیر به دست میآید:
۱۸۰° + “۳۸’۹۴°۱۹ = آزیموت عقب AB
“۳۸’۲۷۴°۱۹ = آزیموت عقب AB
آزیموت عقب و زاویه داخلی را درون رابطه زیر قرار میدهیم:
زاویه بین AB و BC – آزیموت عقب AB = آزیموت BC
“۰۲’۱۴۲°۲۶ – “۳۸’۲۷۴°۱۹ = آزیموت BC
“۳۳’۱۳۱°۵۳ = آزیموت BC
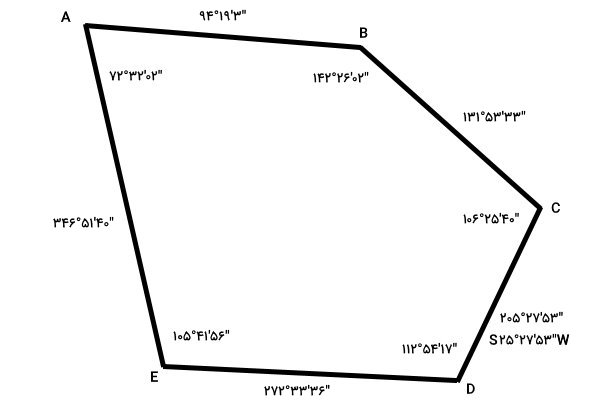
در نتیجه، آزیموت امتداد آخرین خط پیمایش برابر با “۳۳’۵۳°۱۳۱ است. اکنون، به منظور اطمینان از صحت محاسبات، آزیموت امتداد معلوم، یعنی امتداد خط CD را محاسبه میکنیم.
زاویه داخلی بین AB و AB برابر با “۴۰’۲۵°۱۰۶ است. آزیموت عقب امتداد BC به صورت زیر محاسبه میشود:
۱۸۰° + “۳۳’۱۳۱°۵۳ = آزیموت عقب BC
“۳۳’۳۱۱°۵۳ = آزیموت عقب BC
اکنون میتوانیم آزیموت CD را با استفاده از رابطه زیر به دست بیاوریم:
زاویه بین BC و CD – آزیموت عقب BC = آزیموت CD
“۴۰’۱۰۶°۲۵ – “۳۳’۳۱۱°۵۳ = آزیموت CD
“۵۳’۲۰۵°۲۷ = آزیموت CD
آزیموت امتداد خط CD دقیقا با مقدار به دست آمده در ابتدای محاسبات (تبدیل بیرینگ به آزیموت) برابر شد. این نتیجه، صحت محاسبات را تایید میکند.
محاسبه آزیموت خطوط پیمایش در جهت پادساعتگرد
در بخش قبلی، محاسبات آزیموت خطوط را در جهت حرکت عقربههای ساعت به پیش بردیم. امکان انجام محاسبات در خلاف جهت حرکت عقربههای ساعت نیز وجود دارد. در این بخش، قصد داریم با در نظر گرفتن آزیموت امتداد خط DC به عنوان اولین مقدار معلوم، از نقطه C به B، نقطه B به A و نقطه A به E حرکت کنیم و در نهایت به نقطه D برگردیم.
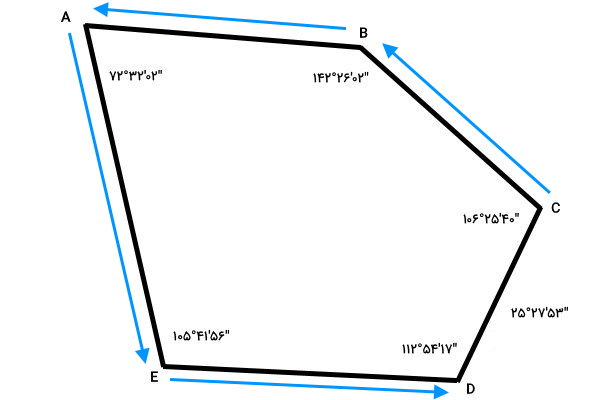
انجام محاسبات را با تعیین آزیموت امتداد خط CB شروع میکنیم. آزیموت امتداد خط DC برابر با “۵۳’۲۷°۲۵ است (توجه داشته باشید که جهت خط عوض شده است). به دلیل پادساعتگرد بودن جهت حرکت، فرمول آزیموت امتداد DC به صورت زیر (فرمول جمع) نوشته میشود:
آزیموت امتداد دوم =
زاویه داخلی بین دو امتداد + آزیموت عقب امتداد اول
زاویه بین DC و CB + آزیموت عقب DC = آزیموت CB
۱۸۰° + “۵۳’۲۵°۲۷ = آزیموت عقب DC
“۵۳’۲۰۵°۲۷ = آزیموت عقب DC
“۴۰’۱۰۶°۲۵ + “۵۳’۲۰۵°۲۷ = آزیموت CB
“۳۳’۳۱۱°۵۳ = آزیموت CB
به همین شکل، آزیموت امتداد خط BA را به دست میآوریم:
زاویه بین CB و BA + آزیموت عقب CB = آزیموت BA
۱۸۰° – “۳۳’۳۱۱°۵۳ = آزیموت عقب CB
“۳۳’۱۳۱°۵۳ = آزیموت عقب CB
“۰۵’۱۴۲°۲۶ + “۳۳’۱۳۱°۵۳ = آزیموت BA
“۳۸’۲۷۴°۱۹ = آزیموت BA
آزیموت امتداد خط AE برابر است با:
زاویه بین BA و AE + آزیموت عقب BA = آزیموت AE
۱۸۰° – “۳۸’۲۷۴°۱۹ = آزیموت عقب BA
“۳۸’۹۴°۱۹ = آزیموت عقب BA
“۰۲’۷۲°۳۲ + “۳۸’۹۴°۱۹ = آزیموت AE
“۴۰’۱۶۶°۵۱ = آزیموت AE
برای آزیموت امتداد خط ED نیز داریم:
زاویه بین AE و ED + آزیموت عقب AE = آزیموت ED
۱۸۰° + “۴۰’۱۶۶°۵۱ = آزیموت عقب AE
“۴۰’۳۴۶°۵۱ = آزیموت عقب AE
“۵۶’۱۰۵°۴۱ + “۴۰’۳۴۶°۵۱ = آزیموت ED
از آنجایی که نتیجه آزیموت بیشتر از ۳۶۰ درجه میشود و آزیموت بزرگتر از ۳۶۰ درجه نداریم، یک عبارت “۰’۰°۳۶۰- به رابطه بالا اضافه میکنیم:
“۰’۳۶۰°۰ – “۵۶’۱۰۵°۴۱ + “۴۰’۳۴۶°۵۱ = آزیموت ED
“۳۶’۹۲°۳۳ = آزیموت ED
در نهایت، به منظور بررسی صحت انجام محاسبات، آزیموت امتداد خط DC را نیز تعیین میکنیم:
زاویه بین ED و DC + آزیموت عقب ED = آزیموت DC
۱۸۰° + “۳۶’۹۲°۳۳ = آزیموت عقب ED
“۳۶’۲۷۲°۳۳ = آزیموت عقب ED
۳۶۰° < “۱۷’۱۱۲°۵۴ + “۳۶’۲۷۲°۳۳ = آزیموت DC
“۰’۳۶۰°۰ – “۱۷’۱۱۲°۵۴ + “۳۶’۲۷۲°۳۳ = آزیموت DC
“۵۳’۲۵°۲۷ = آزیموت DC
همانطور که مشاهده میکنید، آزیموت امتداد خط DC با مقادیر اولیه برابر شد. این نتیجه، صحت محاسبات را تایید میکند. در حین انجام محاسبات و به دست آوردن آزیموتها، همیشه به راستای خطوط در نقشه (نسبت به جهت شمال یا جنوب) و عدد به دست آمده دقت داشته باشید. به عنوان مثال، اگر آزیموت امتداد خط برابر با ۲۵۰ درجه شد، این امتداد، باید در ربع سوم قرار داشته باشد.