در این بخش به منظور آشنایی بهتر و بیشتر با نحوه تحلیل رفتار تیرهای دارای تقارن مضاعف در حین اعمال بارهای مورب، به تشریح دو مثال کاربردی میپردازیم.
مثال 1
شکل زیر، یک تیر یکسر گیردار با طول 12 فوت را نمایش میدهد که مقطع آن از نوع S24*80 است. بار P=10kips در راستای عمودی بر انتهای آزاد تیر اعمال میشود. به دلیل ضخامت کم تیر نسبت به ارتفاع آن، ممان اینرسی حول محور z بسیار بیشتر از ممان اینرسی حول محور y خواهد بود. با در نظر گرفتن اطلاعات مسئله، موارد زیر را تعیین کنید:
- الف) تنش خمشی ماکسیمم با فرض عمودی بودن محور y (همراستا بودن جهت اعمال بار P و محور y)
- ب) تنش خمشی ماکسیمم با فرض وجود زاویه α=1° بین راستای اعمال بار و محور y (توجه داشته باشید که در واقعیت، این زاویه کوچک میتواند بر اثر اشکالات به وجود آمده در حین ساخت تیر، عدم تراز بودن تیر در حین نصب یا جابجایی سازه نگهدارنده ایجاد شده باشد.)

الف) تنش خمشی ماکسیمم در صورت همراستا بودن بار P و محور y
اگر راستای عمودی تیر و جهت اعمال بار به طور کامل با یکدیگر مطابقت داشته باشند، محور z همان محور خنثی خواهد بود. در این حالت، مقدار تنش ماکسیمم با استفاده از رابطه پیچش به دست میآید:

h: ارتفاع تیر؛ Iz: ممان اینرسی حول محور z
به علاوه، Mz=-M=-PL و My=0 است. از اینرو،
M=PL تنش خمشی موجود در محل تکیهگاه خواهد بود. با جایگذاری مقادیر عددی در رابطه بالا، داریم:

این تنش در بالای تیر از نوع کششی و در پایین آن از نوع فشاری است.
ب) تنش خمشی ماکسیمم در صورت وجود زاویه بین بار P و محور y
در بخش دوم مسئله فرض میکنیم که یک انحراف کوچک در راستای تیر وجود دارد. این انحراف باعث ایجاد زاویه α=1° بین محور y و بار P میشود. مؤلفه بار P در راستای منفی y برابر Pcosα و در راستای مثبت z برابر Psinα است. به این ترتیب، برای محاسبه گشتاورهای خمشی موجود در تکیهگاه تیر داریم:

زاویه β (جهتگیری محور خنثی) از رابطه زیر به دست میآید:
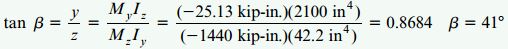
مقدار بالا نشان میدهد که با وجود اختلاف زاویه 1 درجهای بین راستای اعمال بار و محور y، محور خنثی 41 درجه نسبت به محور z اختلاف دارد. حساسیت محل قرارگیری محور خنثی به تغییر زاویه اعمال بار با نسبت Iz/Iy مشخص می شود.
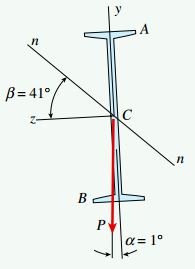
با توجه به موقعیت محور خنثی در شکل بالا، دقت کنید که تنشهای ماکسیمم اعمال شده بر تیر در نقاط A و B رخ میدهند. فاصله این نقاط تا محور خنثی بیشتر از فاصله نقاط دیگر تا این محور است. برای مختصات نقطه A داریم:

به این ترتیب، برای محاسبه تنش کششی موجود در این نقطه خواهیم داشت:

تنش اعمال شده بر نقطه B نیز دارای همین مقدار اما از نوع فشاری است:
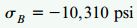
مقدار بالا، 25 درصد از تنش ماکسیمم در بخش اول سؤال (σmax=8230psi) بیشتر است. علاوه بر این، اعمال بار مورب باعث ایجاد اعوجاج جانبی تیر در راستای محور z میشود؛ در حالی که هنگام اعمال بار همراستا با محور y چنین اتفاقی رخ نمیدهد. این مثال نشان میدهد که اگر اختلاف Izبا Iy زیاد باشد، امکان گسترش تنشهای بزرگ در تیرهای تحت بارگذاری مورب حتی با زوایای کوچک نیز وجود دارد. در نتیجه، این تیرها باید با احتیاط کامل مورد استفاده قرار گیرند؛ چراکه در این موارد، احتمال اعمال تنشهای اضافی به بخش جان و کمانش تیر افزایش مییابد. راه حل مقابله با این مسائل، به کارگیری نگهداری مناسب برای کنارههای تیر است. به عنوان مثال، سطوح جانبی تیرچه کفهای چوبی مورد استفاده در ساختمانسازی معمولاً با نصب بلوک در میان تیرچهها نگهداری میشوند.
مثال 2
در شکل زیر، تیر چوبی AB با سطح مقطع مستطیلی به عنوان یک تیرک برای اتصال اجزای سقف مورد استفاده قرار گرفته است. این تیر توسط یالهای بالاییِ دو خرپای مجاور نگهداری میشود. به علاوه، تیر AB در مقابل وزن پوشش و مواد به کار رفته در سقف، وزن خود و بارهای اضافی اعمال شده بر سقف (باد، برف و بارهای لرزهای) مقاومت میکند.

در این مثال قصد داریم تنها تأثیر اعمال یک بار یکنواخت با شدت q=3.0kN/m در جهت عمودی و در محل مرکز هندسی سطح مقطع را در نظر بگیریم. بار مذکور در امتداد طول تیر اعمال شده و وزن آن را نیز شامل میشود.
یالهای بالایی خرپاها دارای شیب 1 به 2 (زاویه α=26.57°) هستند. تیر مورد تحلیل دارای عرض b=100mm، ارتفاع h=150mm و طول L=1.6m است.
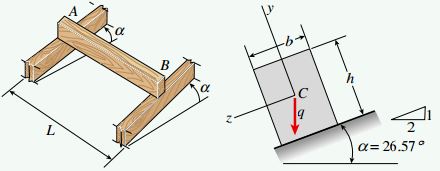
با توجه به اطلاعات مسئله، تنش کششی ماکسیمم، تنش فشاری ماکسیمم و محل قرارگیری محور خنثی را تعیین کنید.
بارها و گشتاورهای خمشی
بار یکنواخت اعمال شده در راستای عمودی را میتوان مطابق شکل زیر به مؤلفههای بار در راستای y و z تجزیه کرد:


گشتاورهای خمشی ماکسیمم در میانه تیر رخ میدهند. مقدار این گشتاورها از رابطه کلی M=qL2/8 به دست میآید. به این ترتیب:
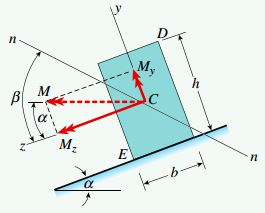

هر دو گشتاور بالا دارای علامت مثبت هستند؛ چراکه جهتگیری بردار آنها به سمت راستای مثبت محورهای y و z است.
ممان اینرسی
ممانهای اینرسی سطح مقطع عرضی نسبت به محورهای y و z عبارتاند از:

تنشهای خمشی
تنشهای موجود در مرکز سطح مقطع تیر از رابطه معرفی شده در ابتدای مقاله (رابطه σx) به دست میآیند. به منظور محاسبه مقدار گشتاور خمشی و ممان اینرسی موجود در این رابطه، از روابط بالا استفاده میکنیم:
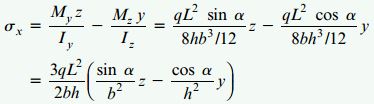
با کمک رابطه بالا میتوانیم مقدار تنش موجود در هر نقطه دلخواه بر روی سطح مقطع تیر را به دست بیاوریم. به این منظور، تنها باید مختصات نقطه مورد نظر را در این رابطه قرار دهیم.

تحلیل تیر
با مشخص بودن جهتگیری سطح مقطع، راستای اعمال بار و امتداد گشتاورهای خمشی (شکل بالا) میتوان مشاهده کرد که تنش فشاری ماکسیمم در نقطه D (با مختصات y=h/2 و z=-b/2) و تنش کششی ماکسیمم در نقطه E (با مختصات y=-h/2 و z=b/2) رخ میدهد. اگر مختصات این نقاط را درون رابطه قبلی وارد کرده و عبارتهای آن را ساده کنیم، روابط مورد نیاز برای تعیین تنشهای ماکسیمم و مینیمم موجود در تیر به دست میآیند:

جایگذاری مقادیر عددی
در ادامه با جایگذاری مقادیر عددی در روابط بالا، مقدار هر یک از پارامترهای مورد نظر را به دست میآوریم.
تنشهای ماکسیمم
تنشهای کششی و فشاری ماکسیمم با جایگذاری اطلاعات زیر در رابطه قبلی محاسبه میشود:

به این ترتیب داریم:

موقعیت محور خنثی
در اغلب موارد، علاوه بر تعیین مقدار تنشهای موجود در تیر، محل قرارگیری محور خنثی نیز مورد بررسی قرار میگیرد. اگر رابطه به دست آمده برای تعیین تنشهای ماکسیمم در بخشهای قبل را برابر با صفر قرار دهیم، رابطه تعیین موقعیت محور خنثی به دست میآید:
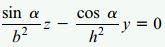
محور خنثی نمایش داده شده در شکل زیر، خط nn است.

تحلیل تیر
زاویه بین محور z و محور خنثی (زاویه β) نیز به صورت زیر محاسبه میشود:
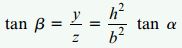
با جایگذاری مقادیر عددی در رابطه بالا، خواهیم داشت:

به دلیل برابر نبودن زاویه β با زاویه α، محور خنثی نسبت به صفحه اعمال بار دارای انحراف است. با توجه به جهتگیری محور خنثی میتوان مشاهده کرد که نقاط D و E (نقاط دارای تنش ماکسیمم) در دورترین فاصله نسبت به محور مذکور قرار دارند. این نکته، فرض رخ دادن تنش تنشهای ماکسیمم در این نقاط را تأیید میکند. تنشهای موجود در قسمت بالا-راست محور خنثی، از نوع فشاری و تنشهای موجود در بخش پایین-چپ محور خنثی از نوع کششی هستند.